Měřený úsek izolačního systému je v praxi tvořen různými konstrukčními částmi, které mají různé kapacity. Výsledná hodnota kapacity (i ztrátového činitele) je tvořena sumou dílčích kapacit (DK). Odvození vztahu pro všechny DK by bylo složité a nepřehledné. Dále je uveden modelový příklad dvou kapacit spojených v sérii (může zastupovat např. kondenzátorovou průchodku s měřícím vývodem) u které jedna kapacita představuje část izolačního systému ve zhoršeném stavu. Byl odvozen vztah [lit.1], ze kterého je patrné, že výsledná hodnota ztrátového činitele tohoto obvodu má vyjádřené maximum, které je dáno poměrem kapacit C1 a C2 (1). Dále platí, že:
Kp = Cp2 / Cp1 (1)
Jestliže změna odporu R reprezentuje změnu kvality DK je patrné, že se zmenšováním velikosti odporu od nejvyšší hodnoty, bude naměřená tg δ stoupat. V konečné fázi, bude-li již velikost odporu R blízká hodnotě rovnající se vodivému spoji, je z obrázku patrné, že kapacita C2 bude z obvodu jakoby odstraněna – zkratována.

Konečná výše ztrátového činitele bude v praxi odpovídat parametrům kapacity C1. Nelze se domnívat, že hodnota tg δ obvodu při zhoršování C2 bude stoupat neomezeně, ale ve skutečnosti dosáhne vrcholu podle vztahu (2). Z dalším zhoršováním obvodu (poklesem hodnoty odporu) dojde i k poklesu ztrátového činitele obvodu, neboť se začne více prosazovat vliv kapacity C1.

Ze vztahu (2) plyne, že maximální hodnota tg δ obvodu je limitována pouze poměrem kapacit Kp. Dále rovněž vyplývá, že u velkých hodnot Kp (poškozená část představuje větší, nebo rozhodující vliv na celkovou kapacitu) budou naměřené hodnoty celku dosahovat vysokých hodnot, které budou samy o sobě při praktickém měření nápadné. Jestliže Kp>>1, pak lze část vztahu (2) upravit na (Kp(Kp))1/2=Kp a maximální naměřená hodnota se prakticky rovná hodnotě 0,5Kp. Poměry při vysokých hodnotách Kp jsou ukázány na obr.1, křivka označená X.
Ve stejném obrázku je znázorněna i křivka, která pro určité Kp ukazuje, jakou konkrétní hodnotu nabude tg δ2, resp. při této hodnotě kapacity C2 bude největší hodnota tg δ celého obvodu. Numerická hodnota tg δ2 opět odpovídá poměru Kp a je dána vztahem (3):

Ze vztahu pro Kp>>1 lze dovodit, že limitní hodnota se rovná 1 a je to i naznačeno na obr.1. Je-li z kapacitního hlediska poškozena velká část dielektrika („množstevně“ tomu může být naopak – ε, l, d).
Kromě nápadně vysokých hodnot tg δ se bude měnit i kapacita (stoupat) a to v intervalu <(C1C2)/(C1+C2) až C1> a její změny budou tím větší, čím menší bude Kp. Tehdy, kdy tg δ obvodu bude dosahovat maxima, bude velikost celkové kapacity dosahovat hodnoty dané vztahem (4).

Odlišná situace nastává u malých hodnot Kp. Ztrátový činitel poškozené části může dosahovat vysokých hodnot, avšak na celkovém projevu hodnoty tg δ obvodu se bude projevovat málo.
Obr.1

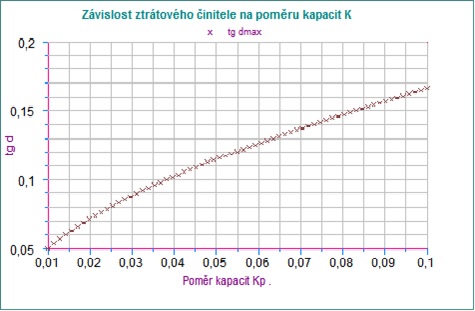
Situaci popisuje Obr. 2. Při Kp = 0,01 sice dosáhne ztrátový činitel poškozené části hodnoty cca 10 (1000 %) avšak tg δ obvodu bude asi 0,05. Při ještě nižších hodnotách poměru kapacit se necitlivost obvodu na lokální poškození projeví ještě méně. U změn celkové kapacity bude situace příznivější, neboť již může znamenat řádové změny.
Obr.2
Výsledná kapacita se bude řídit podle stejného vztahu (4) a platí pro ni i výše uvedený interval.
Lit [1] Ing. A. Barták, CSc, Ing. L. Mravinač, J. Neumann, Ing. J. Vařák, Diagnostika poruch izolací el. strojů. SNTL Praha 1984
Praha 12/2000
